Corso informatica - 1.2 Sistemi di numerazione.

Vi sono due grandi categorie di sistemi di numerazione: sistemi additivi e sistemi posizionali. Nei sistemi additivi il valore della cifra rappresentata si calcola sommando i valori delle cifre che la compongono, esempio il sistema romano; è evidente che in questi sistemi il numero dei simboli usati è illimitato ( I V X L C D M ecc.). es. VIII = V o 5 + I o 1 + I + I = 8.
es. VI = V o 5 + I o 1 = 6.
Nei sistemi posizionali il valore della cifra rappresentata dipende dalla posizione o peso delle cifre che la compongono, (es. i sistemi binario, decimale ed esadecimale). es. 5111 = 5 X 1.000 + 1 X 100 + 1 X 10 + 1 X 1.
es. 51 = 5 X 10 + 1 X 1.
Il nostro sistema di numerazione e detto decimale poiché i simboli usati sono dieci, da 0 a 9.
Il sistema di numerazione binario è composto da 2 simboli o numeri 0 e 1.
Un dispositivo elettronico può facilmente esprimere i valori che indicano due cifre, mentre è quasi impossibile che una macchina riesca a codificare i 10 simboli necessari per la numerazione decimale.
I circuiti del computer riescono a comunicare grazie alla semplicità con cui riescono a rappresentare due stati opposti (interruttore chiuso o aperto, segnale alto o basso, luce accesa o spenta) usando quindi il sistema binario.
Vediamo ora come funziona: supponiamo di avere a disposizione un foglio bianco e di dover scrivere dei numeri avendo a disposizione due soli simboli, 0 e 1.
Per prima cosa bisognerà disegnare dei quadretti ed indicarne il primo (FORMATTARE il foglio).
Per rappresentare zero basterà scrivere 0 nel primo quadretto.
Per rappresentare 1 basterà scrivere 1 nel primo quadretto (il primo quadretto avrà peso 1, 2⁰=1 poiché la numerazione ha soltanto due numeri ed è la prima casella).
Per rappresentare il numero 2 bisognerà scrivere 1 nella seconda casella e 0 nella prima (quindi la seconda casella avrà peso 2, 2¹=2).
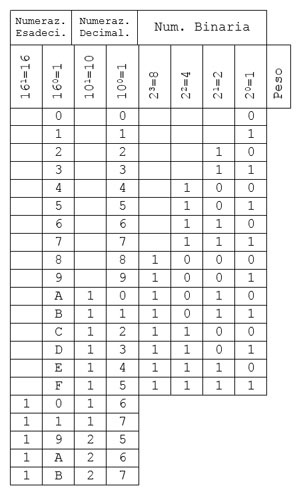
Per rappresentare il numero 3 bisognerà scrivere 1 nella seconda casella e 1 nella prima, e così via come in figura.
Ogni quadretto prende il nome di bit.
Per rappresentare anche le lettere sono stati creati dei codici, basati su questo sistema, lunghi 8 bit cioè un Byte, i più usati sono il codice ASCII ed il codice EBCDIC.
Il sistema di numerazione esadecimale è usato prevalentemente per gli indirizzi di memoria, funziona allo stesso modo del sistema binario, la differenza è che le cifre rappresentabili sono 16 (0 1 2 3 4 5 6 7 8 9 A B C D E F).
La prima cifra ha peso 1, la seconda cifra ha peso 16, la terza cifra ha peso 256 (cioè 16X16), e cosi via. es. FB8 = F o 15 X 256 + B o 11 X 16 + 8 X 1 = 4024
es. F5 = F o 15 X 16 + 5 X 1 = 245
Dall'esempio si vede che passando dall'esadecimale al decimale il numero delle cifre da rappresentare scende. Per scrivere il numero (255) in decimale servono 3 bit, in binario ne servono 8 (11111111) e in esadecimale 2 (FF).

Corso informatica, pag. 1 2 3 4 5 ... 8

Cenni storici  -  Il codice ASCII